보간법 Interpolation 은 영상처리에서 자주 활용됩니다. 이미지 확대나 변환 시 원본 이미지의 특성을 보전하고자 하는 해상도 개선 기법의 기본 입니다. 양선형 보간법 Bilinear Interpolation은 단어에서 같이 선형 보간법을 두번 반복하는 방법이며, 양선형 필터링 또는 양선형 맵핑 등으로도 언급됩니다. 현 블로그에서는 보간법의 이론적인 부분을 간략 다뤄보겠습니다.
양선형 보간 과정을 살펴보면, 그림에서 우리가 알고 싶은 점은 실수 좌표 (x, y)에 위치한 픽셀 값입니다. 이 실수 좌표는 정수 좌표 A, B, C, D의 픽셀 사이에 있으며, 이 정수 좌표의 픽셀 값을 이용하여 보간 할 수 있습니다.
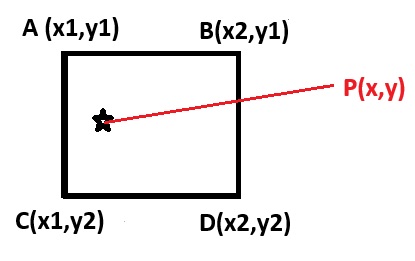
4개의 좌표의 픽셀 값을 식으로 표현하면,
A = f(x1, y1), B = f(x2, y1), C = f(x1, y2), D = f(x2, y2)
보간 위치: (x, y), 여기서 x1 ≤ x ≤ x2, y1 ≤ y ≤ y2
계산 과정을 단계로 보면,
1) X 방향 보간
(A와 B 사이) R1=(x2−x)/(x2−x1)∗A+(x−x1)/(x2−x1)∗B
(C와 D 사이) R2=(x2−x)/(x2−x1)∗C+(x−x1)/(x2−x1)∗D
2) Y 방향 보간
(R1과 R2를 이용) P(x,y)=(y2−y)/(y2−y1)∗R1+(y−y1)/(y2−y1)∗R2
3) 하나의 공식으로 표현하면,
P(x,y)=A∗(x2−x)∗(y2−y)+B∗(x−x1)∗(y2−y)+C∗(x2−x)∗(y−y1)+D∗(x−x1)∗(y−y1)
여기서, 픽셀 간격이 “1”이라고 가정합니다. 참고로 “1”이 아닌 경우 (x2-x1)*(y2-y1)으로 정규화해주는 것이 일반적입니다.
단계별 공식 변환에서처럼 X축 방향과 Y축 방향으로 각각 적용한 방법이 양선형 보간법 입니다. 더 확장해보면 위 식은 다선형 다항식 Multilinear Polynomial 형태로 변환하여 문제를 풀 수 있습니다. 양선형 보간은 이차 다항식이 아니라 두 변수 일차 다항식으로 생각할 수 있으며, 어떤점 (x, y)에서의 값을 2차원이 아닌 일차 다항식 형태로 근사합니다.
하나의 공식으로 합쳐진 P(x, y)를 아래와 같이 좌표 (x, y) 기준 다항식으로 변환 할 수 있습니다.
f(x,y)=a0+a1x+a2y+a3xy
a0=Ax2y2−Bx1y2−Cx2y1+Dx1y1
a1=−Ay2+By2−Cy1+Dy1
a2=−Ax2+Bx1+Cx2−Dx1
a3=A+D−B−C
따라서 위 f(x,y) 식을 선형시스템으로 가정하여 우리가 알고 있는 4개의 위치 A, B, C, D를 행렬식으로 정리하여 선형대수로 계수 a0, a1, a2, a3를 구할 수 있습니다. 간략히 Ax=b 형태의 Matrix 계산으로 변환할 수 있으며, 주변 4개의 좌표를 이용한 양선형 보간법의 예를 파이썬 코드로 확인 할 수 있습니다. 계수 계산 시 np.lianlg,solve 함수를 사용합니다.
| 1 x1 y1 x1y1 | |a0| |f1|
| 1 x2 y1 x2y1 | |a1| = |f2|
| 1 x1 y2 x1y2 | |a2| |f3|
| 1 x2 y2 x2y2 | |a3| |f4|
# Linear System Solution Ax=b
import numpy as np
# 4개 점의 좌표와 픽셀값
x1, x2 = 0, 1
y1, y2 = 0, 1
f1, f2, f3, f4 = A, B, C, D
# 계수 행렬 A
M = np.array([
[1, x1, y1, x1*y1],
[1, x2, y1, x2*y1],
[1, x1, y2, x1*y2],
[1, x2, y2, x2*y2],
])
# 함수값 벡터
f = np.array([f1, f2, f3, f4])
# 계수 a0, a1, a2, a3 계산
a = np.linalg.solve(M, f)
# 양선형 보간 함수
def bilinear_interp(x, y):
return a[0] + a[1]*x + a[2]*y + a[3]*x*y'영상처리 기술' 카테고리의 다른 글
| 영상처리 푸리에 변환 Fourier Transform 이해와 기본 (Python) (0) | 2025.06.01 |
|---|---|
| 영상 처리의 기본 개념: 픽셀, 해상도, 채널, 포맷 (0) | 2025.05.22 |
| 기하학적 이미지 변환 Affine Transform (0) | 2025.04.27 |
| 칼라처리와 특징 Color Processing - RGB, CMY, HSI (0) | 2023.12.03 |
| 이미지 개선 Adaptive Image Enhancement (HE, CLAHE) (0) | 2023.11.12 |
